Der RSA - Algorithmus

Der RSA-Algorithmus

Einleitung

Was ist RSA, was leistet RSA?

Wie funktioniert RSA?

3.1 Grundlagen
3.1.1 Satz von Euler
3.1.2 Euklidscher Algorithmus
3.2 Schlüsselerzeugung
3.3 Verschlüsselung
3.4 Entschlüsselung
3.5 Signatur
3.6 Erläuterndes Beispiel

Vor- und Nachteile

Anwendungsgebiete des RSA - Algorithmus

Beispielprogramm "RSA - Algorithmus"

Biographien der Entwickler

Literaturverzeichnis

1. Einleitung

1976 forderten Whitfield Diffie und Martin Hellman eine neue Art der Verschlüsselungsalgorithmen, sogenannte asymmetrische Chiffrieralgorithmen oder auch public-key-Algorithmen genannt. Bei diesen Verfahren sollte es unmöglich sein mit Kenntnis des Chiffrierschlüssels den Dechiffrierschlüssel zu ermitteln. Die bisherigen symmetrischen Algorithmen hatten zwei wesentliche Nachteile:

1. Schlüsselmanagementproblem:

Jeder Teilnehmer muß mit jedem anderen Teilnehmer einen gemeinsamen Schlüssel vereinbaren. Dadurch werden zum Beispiel bei 1000 Anwendern 499.500 verschiedene Schlüssel notwendig (oder allgemein: bei n Anwendern n(n-1)/2 Schlüssel). Kommt ein neuer Teilnehmer hinzu, muß dieser mit jedem bisherigen Anwender einen eigenen Schlüssel vereinbaren. Dies bedeutet einen erheblichen Aufwand, sobald ein neuer Teilnehmer hinzukommt.

2. Symmetrie zwischen Chiffrier- und Dechiffrierverfahren:

Aus dem Chiffrierschlüssel kann man den Dechiffrierschlüssel ableiten. Dies kommt daher, daß beide Schlüssel entweder identisch oder sehr ähnlich sind. Fängt ein Dritter die chiffrierte Nachricht ab und kennt den Chiffrierschlüssel, kann er die Nachricht auch dechiffrieren.

2. Was ist RSA, was leistet RSA?

Daraufhin entwickelten Ronald Rivest, Adi Shamir und Leonard Adleman 1977 das nach ihnen benannte public-key-Kryptosystem, den RSA-Algorithmus. Er erfüllt die von Diffie und Hellman geforderten Spezifikationen:

- Grundlegende Verschiedenheit zwischen Chiffrier- und Dechiffrierschlüssel
- Der Chiffrierschlüssel wird öffentlich bekannt gegeben, der Dechiffrierschlüssel bleibt geheim.

Dazu ein Beispiel:
Jeder Teilnehmer hat zwei Schlüssel: den Chiffrierschlüssel c und den Dechiffrierschlüssel d. d hält er geheim und c schreibt er in ein "Telefonbuch" - eine Datei, die für jeden zugänglich ist und alle Chiffrierschlüssel c_n enthält. Möchte nun ein Teilnehmer A eine Nachricht an einen Teilnehmer B versenden, sucht er im Telefonbuch nach dem öffentlichen Schlüssel von B (c_B) und verschlüsselt damit seine Nachricht. Nur B kann dann mit seinem geheimen Dechiffrierschlüssel (d_B) diese wieder entschlüsseln. Kommt ein neuer Teilnehmer hinzu, wird nur ein neuer Schlüssel in das Telefonbuch eingetragen. Alle anderen Teilnehmer können sofort mit diesem kommunizieren, da ein Schlüsseltausch wie bei symmetrischen Verfahren nicht erforderlich ist. Es wird lediglich das Telefonbuch aktualisiert.

3. Wie funktioniert RSA?

3.1 Grundlagen

3.1.1 Satz von Euler[vgl. (2)]

Der Satz von Euler lautet:
Sind m und n zwei natürliche teilerfremde Zahlen, so gilt:
m^j
(n) MOD n = 1.

Zur Erklärung definieren wir zunächst folgende Funktion:

j (n)= Die Anzahl der zu n teilerfremden natürlichen Zahlen.

Dementsprechend ist j (n) die Anzahl aller Zahlen (kleiner gleich n), deren größter gemeinsamer Teiler (ggT) mit n gleich 1 ist.

Beispiele:

j (10) = 4 (nämlich 1,3,7,9)
j (11) = 10 (nämlich 1,2,3,4,5,6,7,8,9,10; da eine Primzahl)

Daraus folgt aus der Definition für eine Primzahl - alle Zahlen von 1 bis (p-1) sind teilerfremd zu p: j (p) = p-1.
Hieraus ergibt sich für das Produkt zweier Primzahlen p und q die Beziehung:

j (pq) = (p-1)(q-1)
3.1.2 Euklidscher Algorithmus

Der Euklidsche Algorithmus liefert den grö ßten gemeinsamen Teiler (ggT) zweier natürlicher Zahlen. Er wird beim RSA - Algorithmus zur Berechnung des Codier- und Decodierschlüssels benötigt.
Algorithmus:

Man erhält den ggT zweier natürlicher Zahlen a und b, indem man solange den Rest der Ganzzahlendivision ermittelt, bis der Rest 0 ist. x und y sind Puffervariablen und enthalten zu Anfang die Werte von a und b. Ist der Rest gleich 0, dann ist y der ggT. Solange der Rest ungleich 0 ist, wird x der Wert von y zugewiesen und y erhält den Wert von r.

3.2 Schlüsselerzeugung

Zuerst legt man zwei Primzahlen p und q fest, die für eine sichere Verschlüsselung circa in der Größenordnung 10²⁰⁰ liegen. "Außerdem sollten sich die Stellenzahlen von p und q in der Dezimaldarstellung deutlich unterscheiden, da sich sonst beide Zahlen nur wenig von unterscheiden und durch gezielte Suchalgorithmen (z.B. mit dem Verfahren der Differenz der Quadrate) relativ leicht auffindbar wären." [aus (1), Seite 102]

Als nächstes bestimmt man das Produkt n der beiden Primzahlen und bildet j (n), nach dem Satz von Euler mit .

Nun errechnet man schließlich die eigentlichen Schlüssel c (für Codier – Schlüssel) und d (für Decodier – Schlüssel) durch die Formel:

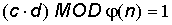
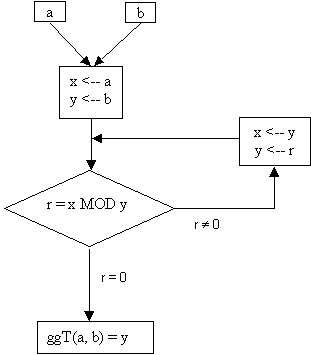
Hierzu wählt man den Schlüssel c so, daß c teilerfremd zu j (n) und daß der ggT(c-1, p-1) und der ggT(c-1, q-1) möglichst klein sind. Um zu erreichen, daß c teilerfremd zu j (n) ist, kann man entweder für c eine Primzahl wählen, die größer als j (n) ist, oder man bestimmt zufällig eine Zahl c kleiner als j (n), für die gilt: ggT(c, j (n)) = 1 (nachzuprüfen mit dem Euklidschen Algorithmus).

Daraus ergibt sich dann der Decodier – Schlüssel d zu:

Da sich bei der Ganzzahlendivision für das Produkt von c und d durch j (n) ein Rest von 1 ergibt, kann man das Produkt von c und d auch als eins plus ein ganzzahliges, positives Vielfaches von j (n) schreiben:

Nun werden n und der Codier – Schlüssel c veröffentlicht bzw. ins "Telefonbuch" eingetragen, d hält der Benutzer geheim und p und q werden vergessen. Es ist fast unmöglich, aus n j (n) zu ermitteln ohne Kenntnis von p und q. Somit ist eine hohe Sicherheit der Verschlüsselung gewährleistet. Bei der Findung von n, c und d ist zu beachten:

Bei verschiedenen Benutzern ist darauf zu achten, daß nicht das selbe n mehrmals vorkommt, da man ansonsten nach dem Lemma von Bachet die Nachricht entschlüsseln kann, wenn sie an zwei Benutzer mit gleichem n geschickt wird. [vgl. (1), Seite 103]

Die ggT(c-1,p-1) und ggT(c-1,q-1) müssen möglichst klein sein, damit die Anzahl der Fixpunkte - dies sind die x von C, für die gilt: x^c= x MOD n, d.h. das ursprüngliche Zeichen entspricht dem verschlüsselten Zeichen - der Abbildung C möglichst klein ist. Denn je mehr Fixpunkte ein Verschlüsselungsalgorithmus besitzt, desto einfacher ist es, ihn zu entschlüsseln. Die Zahl der Fixpunkte berechnet sich aus:

(1 + ggT(c-1,p-1))ž (1 + ggT(c-1,q-1))

3.3 Verschlüsselung

Da nur Zahlen verschlüsselt werden können, wird der zu verschlüsselnde Text t über den ASCII (American Standard Code for Information Interchange) – Code in eine Zahlenfolge konvertiert. Zur Realisierung mittels PC werden diese Zahlen wiederum in einen Binärcode umgewandelt. Dieser wird dann in Blöcken der Reihe nach verschlüsselt (beim ASCII – Code sind die Blöcke zum Beispiel 512 Bit groß).

Die Verschlüsselung funktioniert dann folgendermaßen:

Der Geheimtext g ist der Rest der Ganzzahlendivision aus dem ursprünglichen Text t potenziert mit dem Codier – Schlüssel c des Adressaten und n.

3.4 Entschlüsselung

Die Entschlüsselung erfolgt dementsprechend einfach:

Der ursprüngliche Text t ist der Rest der Ganzzahlendivision aus dem Geheimtext g potenziert mit seinem persönlichen geheimen Decodier – Schlüssel d und n.
Dadurch, daß nur der Adressat über den richtigen Decodier – Schlüssel verfügen kann, ist die Sicherheit der Verschlüsselung gewährleistet.

3.5 Signatur

Weiterhin besteht die Möglichkeit, eine elektronische Unterschrift mit dem RSA-Algorithmus zu realisieren. Hierbei wird das Prinzip der Chiffrierung und Dechiffrierung umgekehrt. Man unterscheidet zwischen

- universelle Unterschrift

Die "Unterschrift" wird mit dem eigenen Dechiffrierschlüssel chiffriert und an den Empfänger versandt. Der Empfänger kann mit Hilfe des öffentlichen Chiffrierschlüssels im Telefonbuch die Chiffrierung wieder rückgängig machen und erhält somit die unverschlüsselte "Unterschrift". Es gilt: c(d(t))=t.

Es kann zwar jeder andere diese Nachricht mit dem öffentlichen Chiffrierschlüssel dechiffrieren, es ist jedoch auch nicht die Absicht, die "Unterschrift" geheimzuhalten, vielmehr soll die Authentizität des Absenders gewähleistet sein.

- nicht universelle Unterschrift

Die mit dem eigenen Dechiffrieschlüssel chiffrierte "Unterschrift" wird zusätzlich mit dem öffentlichen Schlüssel des Empfängers verschlüsselt. Somit wird gewährleistet, daß nur der Empfänger diese Unterschrift entschlüsseln und identifizieren kann.

3.6 Erläuterndes Beispiel [vgl. (2)]

Herr A und Frau B wollen Nachrichten austauschen.

Schlüssel für Herrn A: p=47, q=59

c und d werden berechnet aus der Formel:

Wir wählen c als 17, daraus ergibt sich d zu 157.

Der öffentliche Schlüssel von Herrn A wird also folgendermaßen ins Telefonbuch eingetragen: "A: c_A={17; 2773}". Herr A behält seinen geheimen Schlüssel d_A = 157.

Schlüssel für Frau B: p=71, q=83

c und d werden berechnet aus der Formel:

Wir wählen c als 17, daraus ergibt sich d zu 1013.

Der öffentliche Schlüssel von Frau B wird also folgendermaßen ins Telefonbuch eingetragen: "B: c_B={17; 5893}". Frau B behält ihren geheimen Schlüssel d_B = 1013.

normale Buchstabenverschlüsselung mit

00

F

06

L

12

R

18

X

24

A

01

G

07

M

13

S

19

Y

25

B

02

H

08

N

14

T

20

Z

26

C

03

I

09

O

15

U

21

D

04

J

10

P

16

V

22

E

05

K

11

Q

17

W

23

Herr A möchte die Nachricht "juhu es klappt" codieren für Frau B. Als Zahlencode lautet seine Botschaft:

"10 21 08 21 00 05 19 00 11 12 01 16 16 20".

Nun wird zum Chiffrieren die Botschaft in Blöcke á 4 Ziffern unterteilt, bei denen die Einzelzahlen kleiner als n sind.

Nun sieht Herr A im Telefonbuch nach und findet: c_B={17; 5893}. Er verschlüsselt jeden Block der Nachricht mit der Formel: g = t^c MOD n bzw. hier: g = t¹⁷ MOD 5893 (Formel 3.3). Der Geheimtext g heißt nun:

"5527 3838 4143 4336 2087 4079 5780".

Frau B bekommt die Nachricht und entschlüsselt sie mit der Formel:

t = g^d MOD n bzw. hier: t = g¹⁰¹³ MOD 5893 (Formel siehe 3.4). Als entschlüsselten Text bekommt Sie:

"1021 0821 0005 1900 1112 0116 1620".

Teilt Sie diesen Text in zweistellige Zahlen und übersetzt sie dann mit der Buchstabenverschlüsselung (siehe oben), so erhält sie die Nachricht:

"juhu es klappt".

4. Vor- und Nachteile

Vorteile:

Bei symmetrischen Verschlüsselungsverfahren wie z.B. dem Cäsar-Code mußte immer der Schlüssel (um wie viele Buchstaben das Alphabet verschoben wurde) mit dem Empfänger vereinbart werden. Dies ist bei den asymmetrischen Verschlüsselungsverfahren, wie dem RSA-Algorithmus, nicht der Fall, da es einen öffentlichen und einen geheimen Schlüssel gibt. Ohne Kenntnis des geheimen Schlüssels ist es bis heute noch nicht gelungen, den RSA-Code zu knacken.

Das Schlüsselmanagementproblem wie in der Einleitung beschrieben ist gelöst. Ein neuer Teilnehmer muß sich lediglich in das Telefonbuch eintragen und kann sofort mit allen anderen Teilnehmern kommunizieren, ebenso alle anderen mit ihm.

Die Hauptsicherheit des RSA-Algorithmus liegt darin, daß es praktisch unmöglich ist, aus n die beiden Primfaktoren p und q zu finden, wenn p und q ausreichend groß sind (Größenordnung >10¹⁰⁰). Daraus folgt dann ein n der Größenordnung 10²⁰⁰. Um daraus p und q zu ermitteln, benötigt man mit dem schnellsten heute bekannten Algorithmus ca. 5 * 10⁷ Jahre [siehe (1), Seite 102].

Da die Prozessorgeschwindigkeiten der Rechner rapide ansteigen, ist der derzeit verwendete RSA-Algorithmus wahrscheinlich in absehbarer Zeit von Großrechnern zu entschlüsseln. Um dem entgegenzuwirken vergrößert man einfach die verwendeten Primzahlen um ein paar Bit und erhält somit wieder ein auf längere Zeit sicheres System.

Nachteile:

"Die Sicherheit des Systems beruht auf der Tatsache, daß diese Faktorisierung für genügend große Zahlen selbst mit den größten Computern und derzeit bekannten schnellsten Algorithmen ungeheure Rechenzeiten benötigt und damit praktisch nicht durchführbar ist." [siehe (1), Seite 100]

Diese Sicherheit ist jedoch nur praktisch und nicht theoretisch. Wird ein Algorithmus gefunden, der es ermöglicht, schnell aus n p und q zu folgern, ist der gesamte RSA-Algorithmus geknackt.

5. Anwendungsgebiete des RSA - Algorithmus

1) Netzwerke:
Viele Clients wie zum Beispiel das Novell - System benutzen zur Sicherung ihrer Passwörter den RSA - Algorithmus, da er auf Grund seiner Sicherheit perfekt für diese Anwendung geeignet ist. Die Verwendung von RSA ist sogar eine Art Qualitätsmerkmal für die Sicherheit einer Netzwerkssoftware wie man an dem Bildschirmfoto sieht:

2)Pretty Good Privacy (PGP):
Pretty Good Privacy ist das wohl bekannteste Verschlüsselungsprogramm für den PC. Es verschlüsselt alles von "normalen" Dateien bis zu E-Mails. Auch dieses Programm benutzt den RSA - Algorithmus und ist so sicher, daß es zeitweise verboten war, das Programm von Amerika nach Europa zu exportieren, da es unter das militärische Gesetz zur Spionageabwehr fiel.

3) Chipkarten:
Heute gibt es schon spezielle RSA - Chipkarten, die zum Beispiel PIN - Nummern mit dem RSA - Algorithmus verschlüsseln.

Ein großes Problem des RSA - Algorithmus sind immer noch die hohen Anforderungen, die der Algorithmus an den Rechner stellt. Dies ist zwar einerseits genau der Grund für seine Sicherheit, andererseits aber auch ein Hindernis, um in der Praxis große Datenmengen zu verschlüsseln. Deshalb werden große Datenmengen heute teilweise mit einem symmetrischen Verschlüsselungsverfahren (z.B. DES) codiert. Der Schlüssel selbst, der ja relativ klein ist (zumeist 64 Bit), wird dann mit RSA codiert und übermittelt. Da der RSA - Algorithmus jedoch eine deutlich höhere Sicherheit bietet, werden die Daten wenn möglich immer mit ihm verschlüsselt, was mit der schnell steigenden Rechnerleistung zur raschen Ausbreitung von RSA führt.

6. Beispielprogramm "RSA-Algorithmus"

Um Ihnen dieses theoretische Wissen auch praktisch zu veranschaulichen, haben wir uns die Mühe gemacht, ein kleines Beispielprogramm in Turbo Pascal 6.0 zu entwickeln. Hier steht es Ihnen zum Download bereit: RSA.exe (ca. 25 kB)

Das Programm bietet Ihnen die Möglichkeit, an drei fiktive Personen eine kurze Nachricht mit maximal 80 Zeichen verschlüsselt zu "verschicken" (bzw. in eine Datei zu schreiben). Aus dieser Datei kann man die Nachricht natürlich wieder aufrufen und mit dem richtigen Schlüssel decodieren.

Beim Programmieren ergaben sich mehrere Probleme, da die erforderlichen Rechenanforderungen von Turbo Pascal nicht in diesem Maße erfüllt werden können. Hierdurch mußten wir das Programm sehr stark eingrenzen, das heißt die Sicherheit ist nur minimal, da wir durch die Potenzierung und anschließende Modulo-Berechnung nur Primzahlen <20 verwenden konnten.

Auch wird die Nachricht trotz richtigem Decodierschlüssel teilweise "falsch" entschlüsselt, da die Fixpunkte durch die kleinen verwendeten Zahlen recht häufig als Verschlüsselung entstehen, und dann beim Decodieren nicht richtig umgewandelt werden.

An dem Programm kann man sehen, daß man die Nachricht zwar mit allen Schlüsseln decodieren kann, daß aber nur mit dem richtigen Schlüssel eine sinnvolle Nachricht entsteht. Somit ist die Funktionsweise und Sicherheit des RSA - Algorithmus hier in diesem kleinen Beispielprogramm schon sehr gut zu erkennen.

7. Biographien der Entwickler

Leonard Adleman: