Entfernungsbestimmung in der Astronomie

Inhalt:

• Beispiele typischer Entfernungen

• Methoden der Entfernungsbestimmung

• Die trigonometrische Parallaxe

• Die spektroskopische Parallaxe

• Die Hyaden

• Die Cepheiden

• Statistiken

• Die Hubblekonstante

Beispiele typischer Entfernungen

Sonne, Erde, Mond

 Der Bereich des Sonnensystems

Verwenden wir zur Veranschaulichung des maximalen Abstandes von Pluto zur Sonne den Abstand Anstoßpunkt - Tor auf einem Fußballfeld, so ergibt sich folgendes Bild:

 Die Nachbarn der Sonne

In diesem Modell ist Pluto ca. 28 m vom Ausgangspunkt entfernt, die Sonne hat einen Radius von 6 mm.

Unsere Galaxie

ist eine Spiralgalaxie. Die Sonne steht nicht im Zentrum, sondern in einem der Seitenarme. Im folgenden sind in einer Seitenansicht die Größenordnungen dargestellt:

Eine mögliche Seitenansicht und ein Blick von oben auf die Spiralarme könnte so aussehen:

 © Space Telescope Science Institute  

Die Nachbargalaxien

In einem Radius von ca. 700 kpc um unsere Milchstrasse finden sich etwa 20 meist kleinere Galaxien. Man nennt diese Ansammlung die lokale Gruppe. Die Daten der wichtigsten Mitglieder sind:

Dies zeigt schon, dass Galaxien häufig in Gruppen, sogenannten Galaxienhaufen vorkommen. Die lokale Gruppe bildet wahrscheinlich eine kleine Gruppe am Rande des Virgohaufens.

Galaxienhaufen

Methoden der Entfernungsbestimmung

 Die trigonometrische Parallaxe

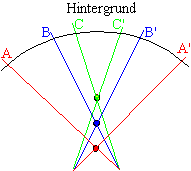Beobachten wir einen nahen Gegenstand von verschiedenen Orten aus, so scheint der Gegenstand seine Position vor dem sehr weit entfernten Hintergrund zu ändern. (Beobachten sie z.B. den Zeigefinger, den sie vor die Nase halten einmal nur mit dem linken und einmal nur mit dem rechten Auge !).

Ebenso sehen wir, dass besonders nahe Sterne ihre Position vor dem Hintergrund der sehr weit entfernten Sterne verändern, wenn wir unsere Position verändern. Natürlich ist diese Positionsänderung auch für die größtmögliche Ortsveränderung sehr klein und daher schwierig zu messen. Die größte Ortsveränderung, die wir ausführen können, ist doppelt so groß wie die große Halbachse der Erdbahn, d.h. wir messen im zeitlichen Abstand von einem halben Jahr. In einer Skizze sieht das so aus:

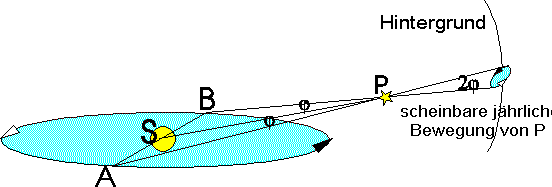
 Wir verbinden P mit der Sonne S. A und B sind die Positionen der Erde mit halbjährlichem Abstand, die zu PS orthogonal sind. Die Entfernung zur Sonne ist also (wegen der geringen Exzentrizität der Erdbahn) in sehr guter Näherung 1 AE. Der Winkel j , unter dem man den mittleren Abstand Sonne-Erde vom Stern P aus sehen würde, heißt Parallaxenwinkel oder einfach jährliche oder trigonometrische Parallaxe. Er ist um so kleiner, je weiter der Stern entfernt ist. Im Laufe des Jahres beschreibt der Stern von der Erde aus gesehen eine Ellipsenbahn vor dem Hintergrund der sehr weit entfernten Sterne (mit nicht feststellbarer Parallaxe).

Im rechtwinkligen Dreieck APS gilt:

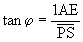
Für die auftretenden kleinen Winkel gilt tan j = j , wenn wir j im Bogenmaß messen. Bezeichnen wir die Entfernung des Sterns mit r, so gilt dann:

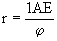
Ist der Winkel halb so groß, so ist die Entfernung doppelt so groß. Man führt nun eine neue Entfernungseinheit ein, es ist die Entfernung, für die die Parallaxe 1" betragen würde. Die Entfernung heißt dann 1 Parallaxensekunde, kurz 1 Parsec (1 pc).

Durch die Umwandlung ins Bogenmaß ergibt sich

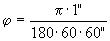
und damit

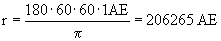
Damit ist 1 pc = 206265 AE und die Entfernung kann mit

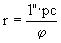
mit j im Gradmaß (in Sekunden) berechnet werden.

Beispiel: Gilt j = 0,5", so ist r = 2 pc, gilt j = 0,1", so ist r = 10 pc.

Die größte gemessene Parallaxe, also die des Nachbarsterns der Sonne, Proxima Centauri, beträgt nur 0,7687". Die anderen Parallaxen sind noch viel kleiner und daher schwierig zu messen. Ab einer Entfernung von ca. 1000 pc versagt die Methode selbst bei hellen Sternen (Stand 2015, Satellit Hipparcos), da die Parallaxen dann so klein sind, dass sie im Bereich der Messfehler liegen.

Für weiter entfernte Sterne ist eine geometrischen Entfernungsbestimmung also nicht mehr möglich, man muss sich andere Methoden ausdenken.

Die spektroskopische Parallaxe

Der Strahlungsstrom des Lichtes, die wir von einem Stern empfangen, seine Helligkeit hängt nicht nur davon ab, wie stark der Stern leuchtet, sondern auch von seiner Entfernung. Ein sehr schwach leuchtender Stern in der Nähe kann uns am Himmel heller erscheinen als ein sehr leuchtkräftiger Stern, der sehr weit entfernt ist.

Der Strahlungsstrom des von einem Stern empfangenen Lichtes nimmt nach dem Energiesatz mit dem Quadrat der Entfernung ab, da sie sich in doppelter Entfernung auf eine Kugel mit 4-facher Oberfläche verteilt. Kennt man also die Leuchtkraft eines Objektes, so kann man aus dem Strahlungsstrom, den wir auf der Erde empfangen (aus der scheinbaren Helligkeit) die Entfernung des Objektes bestimmen.

Um ein Maß für die wahre Helligkeit eines Objektes zu haben, bringt man die Objekte in dieselbe Entfernung. Man wählt dafür 10 pc. Die aus dieser Entfernung auf der Erde gemessene scheinbare Helligkeit heißt dann absolute Helligkeit M des Objektes.

Ist S(10pc) der Strahlungsstrom des abgestrahlten Lichts in 10 pc Entfernung, so gilt für den Strahlungsstrom S(r), der in der Entfernung r gemessen wird:

Andererseits gilt für das Verhältnis der empfangenen Strahlungsströme nach Definition der scheinbaren Helligkeit

Durch Gleichsetzen erhält für die Entfernung:

m-M heißt auch Entfernungsmodul.

Die obige Gleichung kann für die Entfernungsbestimmung natürlich nur dann eingesetzt werden, wenn man neben der (einfach zu bestimmenden) scheinbaren Helligkeit m auch die absolute Helligkeit M des Objektes kennt.

Bei der Bestimmung von M geht man daher von zusätzlichen Annahmen aus. Z.B. entspricht das Spektrum des fernen Objektes genau dem eines nahen Objektes, von dem man mittels der trigonometrischen Parallaxe die Entfernung und damit die absolute Helligkeit bestimmen konnte. Man kann dann annehmen, dass die absoluten Helligkeit des fernen Objektes mit der des nahen übereinstimmt.

Die so erhaltene Parallaxe heißt auch spektroskopische Parallaxe. Man kann sie bis zu so großen Entfernungen verwenden, wie man die Spektren noch klar zuordnen kann. Für größere Entfernungen geht das jedoch nicht mehr.

Letztlich beruht diese Methode also auch auf der trigonometrischen Entfernungsbestimmung, da man die Entfernung der Vergleichsobjekte kennen muss.

Die Hyaden

Eine Gruppe von mehr als 100 Sternen im Bereich des Sternbildes Stier. Sie zeigen eine deutliche Eigenbewegung auf einen Konvergenzpunkt im Sternbild Orion hin. Dies ist ein perspektivischer Effekt, in Wirklichkeit bewegen sich die Sterne parallel und entfernen sich von uns. Die parallele Bewegung erscheint von der Erde aus wie die Konvergenz zu einem Punkt (vgl. zwei parallele Eisenbahnschienen).

Mit Hilfe des Dopplereffekts kann man die Radialgeschwindigkeiten der Mitglieder dieser Gruppe bestimmen. Ferner kennen wir den Winkel j zwischen der wahren Geschwindigkeit v und der Radialgeschwindigkeit v_r, denn das ist der Winkel zwischen dem Sternort und dem Konvergenzpunkt K. v_s ist die Geschwindigkeit senkrecht zur Blickrichtung.

Im rechtwinkligen Geschwindigkeitsdreieck können wir aus j und v_r die Geschwindigkeit v_s bestimmen: v_s = v_r tan j . Legt der Stern in der Zeit t scheinbar aufgrund von v_r den Winkel a zurück, so gilt (im Bogenmaß) in guter Näherung a = v_s t/r. Kennt man also t und den zugehörigen Winkel der Eigenbewegung, so kann man den Abstand r bestimmen.

Für die Hyadensterne ergibt sich r = 42 pc, die Entfernungen der Sterne dieser Gruppe schwanken um ca. 5 pc. Damit hat man eine große Gruppe verschiedener Sterne bekannter Entfernung, an die man die Messung der spektroskopischen Parallaxe anschließen kann.

Die Cepheiden

Bei einigen Gruppen veränderlicher Sterne hat man festgestellt, dass die Periode, mit der sich die Sternhelligkeit ändert, mit der absoluten Helligkeit der Sterne zusammenhängt. Beispiele sind die RR-Lyrae-Sterne, deren (mittlere) absolute Helligkeit nahezu konstant ist und die Cepheiden, mit einer bekannten Perioden-Leuchtkraft-Beziehung.

Kann man einen Stern als zu einem dieser Typen gehörend identifizieren, so kann man aus der Periodendauer die absolute Helligkeit und damit seine Entfernung bestimmen.

Kann man in einer Galaxie noch einen dazugehörenden Cepheiden auflösen, so kennt man die Entfernung der Galaxie.

Die Methode muss natürlich zuerst an einem Cepheiden bekannter Entfernung geeicht werden. Leider findet man in den Hyaden keinen Cepheiden, wohl aber in bestimmten Sternhaufen. In diesen Sternhaufen findet man auch Sterne, deren Spektrum mit einem Stern der Hyaden verglichen werden kann (spektroskopische Parallaxe). Somit kennt man die Entfernung dieses Mitgliedes eines Sternhaufens und damit auch die des Cepheiden.

Statistiken

Findet man in Galaxien keine Cepheiden, so greift man auf andere Standardkerzen zurück. So kann man zum Beispiel annehmen, dass die hellsten Sterne einer aus vielen Milliarden Sternen bestehenden Galaxie wohl immer gleich aufgebaut, d.h. auch gleich hell sind. Diese Methoden muss man natürlich an Objekten eichen, die noch im Bereich der Cepheidenmethode liegen.

Ebenso bilden Supernovaexplosionen eine andere Möglichkeit, wenn man den Helligkeitsverlauf einer solchen Explosion in Abhängigkeit von der Zeit an genügend vielen anderen Beispielen aufgeklärt hat.

Natürlich sind diese Methoden mit größeren Unsicherheiten verbunden.

Die Hubblekonstante

Um das Jahr 1912 konnte man erstmals die Radialgeschwindigkeiten von Galaxien mit Hilfe des Dopplereffekts bei dem von ihnen ausgestrahlten Licht messen (Rotverschiebung). Die Galaxien bewegen sich alle (mit Ausnahme einiger der lokalen Gruppe) von uns weg. Der Astronom E. Hubble konnte mit den oben angegebenen Methoden auch die Entfernungen von einem Dutzend dieser Galaxien bestimmen und stellte (für damals 24 Galaxien) fest, dass die Radialgeschwindigkeit zur Entfernung proportional ist. D.h.: je weiter die Objekte entfernt sind, um so größer ist ihre Radialgeschwindigkeit.

v = H × r

Die Konstante (?) H heißt Hubblekonstante. Hubble gab ursprünglich 500 km s^-1/Mpc an. Bisher mussten die Entfernungen aber mehrfach (zu größeren Werten) korrigiert werden, wodurch sich die Hubblekonstante stets verkleinerte. Zur Zeit ist der Wert 74 km s^-1/Mpc. Kennt man die Radialgeschwindigkeit der Galaxie, die aus dem Dopplereffekt relativ einfach zu bestimmen ist, so kann man mit einer Hubbelkonstante (nach Wahl) auch die Entfernung ausrechnen.

zum Index