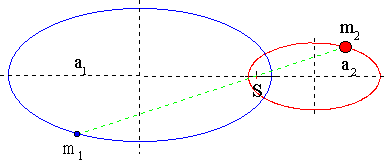

Die beiden Ellipsen sind ähnlich und für die großen Halbachsen gilt:
(Im gezeichneten Beispiel ist m2 = 2 m1)
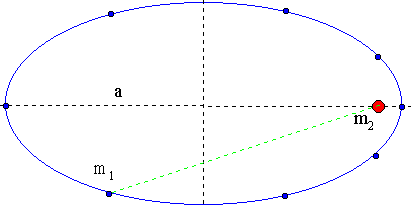
Die Bewegung der beiden Sterne um den Schwerpunkt S des Systems ist sehr schwer zu beobachten, einfacher ist es die relative Bahn eines Sterns in Bezug auf den anderen zu registrieren. Diese Bahn ist ähnlich zu den beiden oben gezeichneten Ellipsen.
Für die relative Bahn gilt nach dem 3. Keplerschen Gesetz:
Dabei ist a die große Halbachse der relativen Bahn in AE, T die Umlaufzeit in Jahren und m1+m2 die Massensumme in Sonnenmassen.
Die Schwerpunktbedingung m1(a1+e1)= m2(a2+e2) liefert mit (e1/a1) = (e2/a2) - da die Ellipsen ähnlich sind - die Beziehung
(e1, e2 sind die linearen Exzentrizitäten, d.h. der Abstand des Brennpunktes der Ellipse vom Mittelpunkt)
Für die Bestimmung der Sternmassen ist die Umlaufzeit T einfach zu bestimmen. D.h. kann man die große Halbachse der relativen Bahn bestimmen, die ja im Normalfall durch die schräge Lage im Raum verzerrt ist, so erhält man die Massensumme der beiden Sterne.
Für die Bestimmung der Einzelmassen benötigt man beide großen Halbachsen der Bahnen um den Schwerpunkt des Doppelsternsystems. Diese sind im Normalfall sehr schwierig zu bestimmen. Fallen die Messwerte in den Bereich der Messungenauigkeit, so benötigt man eine weitere Relation zwischen den Sternmassen, um die beiden Massen zu bestimmen. Hier kann - wenn beide Sterne Hauptreihensterne sind - z.B. die Masse-Leuchtkraft-Beziehung L ~ m3 verwendet werden. Da die Sterne die nahezu gleiche Entfernung von der Erde haben, kann das Verhältnis der Leuchtkräfte sogar mit Hilfe der scheinbaren Helligkeiten bestimmt werden.