Sternradien

Übersicht

• Radius der Sonne
• Radiusbestimmung bei Bedeckungsveränderlichen
• Radiusbestimmung aus dem Gesetz von Stefan-Boltzmann

Radius der Sonne

Wenn das Sonnenbild einen der Kreise von innen berührt, starten wir die Uhr, wenn derselbe Kreis von außen berührt wird, stoppen wir die Uhr. In der gestoppten Zeit legt die Sonne genau den Winkel zurück, unter dem wir die Sonnenscheibe sehen.

Wenn die Sonne auf dem Himmelsäquator steht (Frühlingspunkt, Herbstpunkt) ist ihre Winkelgeschwindigkeit 360⁰/24h = 0,25'/s. Hat die Sonne die Deklination d , so ist ihre Winkelgeschwindigkeit 0,25'/s  cos d. (Nachweis !)

Daraus ergibt sich der Winkel, unter dem wir die Sonnenscheibe sehen und mittels der Entfernung Sonne-Erde der Durchmesser der Sonne.

Bedeckungsveränderliche

Der folgende Spezialfall zeigt das Prinzip:

Ist v der Betrag der Bahngeschwindigkeit (Kreisbahn) des kleinen um den großen Stern, D der Durchmesser des großen, d der Durchmesser des kleinen Sterns, so gilt:  Damit ergibt sich:  D.h.: Die Durchmesser der Komponenten sind einfach zu bestimmen, wenn man den Betrag der Umlaufgeschwindigkeit v kennt.  Dieser kann z.B. aus dem Dopplereffekt (Verschiebung der Spektrallinien) bestimmt werden.

Hier wurden folgende Vereinfachungen verwendet:

• Die Umlaufebene des Doppelsternsystems ist nicht gegen die Beobachtungsrichtung geneigt.
• Die Umlaufbahn ist eine Kreisbahn. (Konstanter Betrag der Umlaufgeschwindigkeit)
• Der "große" Stern wurde festgehalten. In Wirklichkeit bewegen sich beide Sterne um den gemeinsamen Schwerpunkt.

Beta Lyrae 1992-1993

Radiusbestimmung mit dem Stefan-Boltzmann-Gesetz

Da die Oberfläche eines (kugelförmigen) Sterns 4p R² beträgt, ist die pro Sekunde insgesamt abgestrahlte Energie bei der Oberflächentemperatur T, d.h. die Leuchtkraft L daher

Vergleicht man die Leuchtkraft L eines Sterns mit der Leuchtkraft L_S der Sonne, so erhält man:

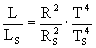    (1)

Bringt man beide Sterne in die gleiche Entfernung, so ist der Strahlungsstrom, der von einem Empfänger registriert wird, proportional zu Energie, die pro Sekunde abgestrahlt wurde, d.h. zur Leuchtkraft L. Wegen

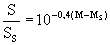
ergibt sich

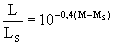   (2)

Dabei ist M die absolute bolometrische (d.h. über alle Wellenlängen gemessene) Helligkeit des Sterns, M_S der entsprechende Wert der Sonne.

Aus (1) uns (2) lässt sich der Radius R des Sterns in Sonnenradien R_S berechnen:

Beispiel: Folgende Werte sind bekannt:

Nun zum Radius:

Der Sternradius beträgt also 0,75 Sonnenradien oder R = 0,75 × 696 000 km = 522 000 km.