Datenbanktaktiken - Sinnvolle Alternativen zur Spieltheorie ?

minimale Spieltaktiken am Beispiel NimmSpiel

Diese Seite behandelt eine Computertaktik in einem ziemlich simplen Streichholzspiel. Beschrieben wird wie wir in der Klasse gemeinsam die Grundzüge für die Taktiken für den Computer entwarfen, die Taktik selbst wird beschrieben und anhand eines Diagramms näher erläutert. Des weiteren werden die im Algorithmus verankerten Probleme erläutert. Zusätzlich ist es möglich den Quelltext einzusehen, Screenshots zu betrachten oder das gesamte Programm down zu laden.

Gliederung:

1.                                         Das NimmSpiel

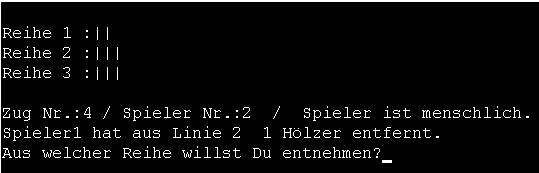
Das NimmSpiel ist ein Streichholzspiel für zwei Spieler. In 3 verschiedenen Reihen liegen jeweils einmal 3 , 4 und 5 Hölzer. Die Spieler entfernen nun abwechseln eine beliebige Anzahl von Hölzern. Sie müssen sich da bei jedoch immer auf nur eine Reihe beschränken. Sie können also nicht ein Holz aus Reihe 1 und eins aus Reihe 2 ziehen. Ebenfalls besteht Zugzwang. Pro Runde muß jeder Spieler mindesten ein Holz entfernen bis keine mehr vorhanden sind.
Ziel des Spiels ist es, das vorletzte Hölzchen zu entfernen. D.h. derjenige, der das letzte Holz entfernt, hat verloren.                                                                                                                                                                 

 2.                                                          Computertaktik

2.1                                               Beschreibung der Computertaktik

2.1.1                                                Entstehung und Vorüberlegungen in der Klasse

Von Herrn Schmitt ging die Idee aus, ein Gesellschaftsspiel auf dem Computer umzusetzen und selbst zu programmieren.
Das Grundgerüst zu realisieren erwies sich als relativ einfach:
Nach einem geeignetem Hauptmenue, in denen man die Spielerkombinationen (Mensch VS Mensch), (Mensch VS Computer) oder (Computer VS Computer) auswählen kann, und diese entsprechend zugeordnet wurden. Wird die Prozedur zum Spielablauf gestartet, eine Repeat-Schleife mit folgenden Funktionen: 

	Aufbau / Aktualisierung des virtuellen Spielbretts
	Einlesen bzw. Errechnen der Züge des Spielers bzw. des Computers
	"reale" Umsetzung des Zuges (in Form von Subtraktion)
	erneuter Bildschirmaufbau mit Kommentar
	Überprüfung, ob das Spiel von einer Partei gewonnen wurde

Dieser Ablauf ist so für jeden beliebigen Spieler gleich. Die Spieler selbst, gespeichert in einer Feldvariablen, wurden durch den Rest der Division (Anzahl Züge) / (2) bestimmt.
Das einzige Problem stellte sich in der Frage, wie man die Züge des Computers, außer durch Zufall, realisieren könne. Die wohl einzigsten Vorteile, die dem PC, im Vergleich zum Menschen, zu Verfügung stehen, sind die Fähigkeiten sehr schnell mathematische Funktionen zu durchlaufen sowie große Datenmenge sekundenschnell zu verwalten und stets präsent zu haben. Also mußten wir versuchen diese Vorteile gegen das taktische Denkvermögen in mehreren Stufen einzusetzen.

Unsere Idee war es nun, den Computer per Zufall ziehen zu lassen, sich jedoch den "tödlichen", letzten Zug immer zu merken.
Sollte ein Spieler verlieren, so wird automatisch der letzte Spielbrettaufbau, sowie der letzte Zug in einer Datei gespeichert.

Vor jedem Zug wird der Computer also erst seine Datenbank durchsuchen, und überprüfen, ob bei dem gegebenen Spielstand schon einmal ein zur Niederlage führender Fehler begangen wurde. Findet er keinen Eintrag zu dem aktuellen Spielstand, wird er jedoch wieder nach den Zufallsprinzip ziehen. Findet er einen Eintrag, so wird er einen anderen, noch nie versuchten Zug auswählen.
Nach dem Prinzip "Übung macht den Meister" wird der Computer immer besser werden, da er NIE den selben Fehler 2x machen wird.                                                                                                                 

2.2.2                                       Exakte Beschreibung der Computertaktik

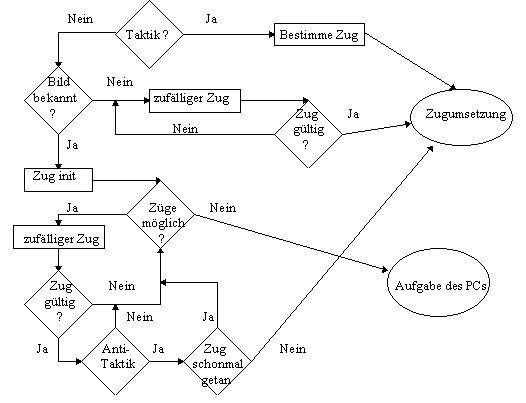
Wir beginnen in einem beliebigen Zug. Auf dem Spielbrett befindet sich eine beliebige Kombination von Streichhölzern.
Nun wird der Computer nach folgender Reihenfolge vorgehen und so seinen Zug bestimmen: 

1. Zuerst wird über geeignete Funktionen das Spielbrett "gescannt" und dem PC mitgeteilt, wieviele Reihen keine, ein oder mehr als ein Streichholz besitzen. Mit Hilfe dieser Informationen sucht der PC nun nach möglichen Kurzstrategien, die von mir vorher programmiert worden sind. Bsp.: Ist eine Reihe leer, eine voll und eine nur mit einem Holz besetzt, so wird er die volle Reihe sofort komplett räumen und damit gewinnen. Diese Option erkennt also nur Taktiken, welche sofort zum Sieg führen. Wird eine solche erkannt, so wird der Zug bestimmt und, falls regelgerecht, ausgeführt. =>ENDE

2. Wenn keine Grundtaktik erkannt wird, so sucht der PC in seiner Datenbank nach dem aktuellen Spielaufbau. Findet er keinen Eintrag, so wird er solange zufällige Züge bestimmen, bis einer von ihnen regelkonform ist. =>ENDE

3. Findet er aber einen Eintrag, so wird er die Variablen für die Reihe auf 3 und die Variable für die Hölzer auf 6 setzen.

4. Die folgenden Züge werden jetzt der Reihe nach abwärts geprüft: 5,3 ; 4,3 ; 3;3 ..... wenn die erste Variable (Hölzer) den Wert 0 hat, so wird die zweite Variable (Reihe) um 1 vermindert und die erste Variable entsprechend erhöht. Jedesmal, wenn dieser Punkt aufgerufen wird, wird der Zug "vermindert", bis entweder (0,0) erreicht ist, oder der Zug angenommen wird.

5. Der aus 4. bestimmte Zug wird jetzt daraufhin überprüft, ob er real durchführbar ist, d.h. ob nicht existierende Hölzer entfernt werden sollen, ob überhaupt Hölzer entfernt werden sollen, ob die Reihe überhaupt existiert. Ist der Zug nicht zugelassen, wird unter 4. der nächste ausgewählt. Ist der Zug auf (0,0) abgesunken oder zugelassen worden, so geht es bei 6. weiter.

6. Jetzt wird überprüft, ob der ausgewählte Zug dem Gegner ebenfalls eine Kurztaktik ermöglicht. D.h. jeder Zug, der eine Kurztaktik ermöglicht wird sofort abgelehnt und es wird unter 4. ein neuer Zug ausgewählt. Wird der Zug zugelassen oder ist er auf (0,0) abgesunken geht es weiter bei 7.

7. Letztendlich wird jetzt in der Datenbank gesucht, ob zu dieser Spielbrettkonstelation auch schon dieser Zug gespeichert wurde. Wird dieser Zug schon gefunden, so hat er schon einmal zur Niederlage geführt und wird nicht zugelassen. Wird der Zug zugelassen oder ist er auf (0,0) abgesunken geht es weiter bei 8.

8. Da nun alle Prüfungen bestanden sind, wird dieser Zug nun an als richtig anerkannt und an die Prozedur zur realen Umsetzung weitergegeben. => ENDE Lautete der Zug jedoch (0,0), so ist dies das Zeichen, daß es keinen möglichen Zug mehr gibt. Als Folge daraus gibt der Computer auf.                                                                                                                                             

2.2        Flußdiagramm zur Computertaktik

Punkte 2.3 und 2.4 sind aus Platzgründen am Ende dieser Seite gespeichert


3.                                                                Diskussion

3.1                                                         Algorithmisch bedingte Probleme

So schön diese Taktik für einen Laien wie mich auch aussieht, sie birgt dennoch erhebliche Probleme:

	Diese angebliche und doch so hoch gelobte Taktik ist leider doch nichts anderes als ein Zufallsprodukt. Jeder neue Zug, aus dem gelernt werden könnte, wird durch Zufall bestimmt. Auch entscheidet der PC nicht selbst nach bestimmten Kriterien, sondern folgt lediglich der sturen Anordnung aller möglichen Züge, bis er einen findet.
	Auch ist es keine Taktik sondern lediglich ein dummes Herumprobieren. In Wirklichkeit entscheidet er nicht, was er tut oder nicht, sondern er tut nur nicht, was er früher schon einmal getan hat. (Schönes Deutsch!) Was ich sagen will: Es ist kein Denken, sondern ein Probieren.
	Die von mir programmierte Kurztaktik ist ebenfalls nur sehr klein. Sie stellt eigentlich auch keine Taktik dar, sie erkennt lediglich die Chance direkt zu gewinnen. Eine Taktik beinhaltet normalerweise ein Vordenken.
	Da es keine direkte Taktik bzw. keinen Denkapparat gibt, ist es unmöglich verschiedene Schwierigkeitsstufen zu programmieren. Lediglich die Größe der Datenbank ist variabel. Das ist jedoch ist nicht mit Schwierigkeitsstufen vergleichbar.
	Ein weiteres Problem ist die große Datenmenge, die bei jedem Zug mehrmals durchsucht werden muss. Beim NimmSpiel ist das kein Problem, bei komplexeren Spielen, wie z.B. Schach, wo viel mehr Spielbrettkonstellationen und pro Spielbrett viel mehr Zugkombinationen durchsucht werden müssen, wird der Rechner zu viel Zeit brauchen. Damit würde er die Geduld des Gegenspielers, sowie die eventuelle maximale Bedenkzeit, bei weiten überstrapazieren.
	Ein weiteres Manko ist die Unflexibilität des Algorithmusses. Er kann auf kein komplexes Spiel übertragen werden, sondern muss dafür komplett neu geschrieben werden. Auch ist die Frage, wie mein Programm auf Zufälle einer dritten Partei (Würfel, Ereigniskarten) reagieren soll.
	Es gibt jedoch noch ein viel größeres Problem, welches unwiderruflich mit dem Algorithmus verbunden ist, und ihn somit disqualifiziert und unbrauchbar macht: Das NimmSpiel ist so konzipiert, daß man jederzeit und unter jeden Bedingungen gewinnen kann. Für den Algorithmus bedeutet dies, dass er bei jedem Zug geschlagen werden kann. Also wird er sich früher oder später jeden Zug gemerkt haben und deswegen direkt zu Beginn des Spiels aufgeben, ohne auch nur einen einzigen Zug gemacht zu haben.

3.2                                          MINIMAX im Vergleich zu meiner Taktik

Der MINIMAX-Algorithmus ist, im Gegensatz zu meinem, ein vollwertiger Algorithmus, der auf fast jedes Spiel anwendbar ist. Durch eine Vielzahl von Zusatzfunktionen wird er sogar vergleichbar mit einem menschlichem Spieler und dessen aufgebrachter Denkleistung.
Das Grundprinzip ist einfach: Er stellt einen Suchbaum mit allen möglichen Ereignissen und Folgeereignissen auf. Sogar Zufallsereignisse, wie z.B. der Würfelwurf werden mit einbezogen. Anschließend werden die einzelnen Bäume mit Hilfe einer Nutzenfunktion bewertet und der Zug mit dem günstigsten Ergebnis ausgewählt.
Um die auftretenden Rechenarbeiten zu vermindern, wird statt der Nutzenfunktion eine Bewertungsfunktion eingeführt, welche die Suchbäume frühzeitig abbricht und dann bewertet. Mit Alpha-Beta-Pruning wird verhindert das jeder Knoten durchsucht wird und nurnoch die Knoten mit besseren Chancen betrachtet werden. Mit Hilfe aller dieser Komponenten kann ein durchschnittlicher PC mit MiniMax ausgerüstet sich ohne Probleme mit einem Menschen messen.
Im Vergleich zu meinem Algorithmus würde das Hauptproblem nicht mehr auftreten. Man könnte über eine entsprechende Bewertungsfunktion Schwierigkeitsstufen programmieren und die Rechenzeit ist regulierbar. Auch hätte diese Taktik nicht mehr mit Zufall zu tun und bräuchte auch keine Kurztaktik durch den Programmierer. Vorallem wäre ein logisches Vordenken realisiert und somit dem Anspruch einer Taktik entsprochen.

Weitere Informationen zu diesem Thema  findet man bei meinem Kamerad Michael.

4.                                             Ergebnis meiner Recherche

Zusammenfassend kann gesagt werden, daß mein Algorithmus zwar ein Einstieg in die KI-Programmierung ist. Jedoch liefert der Algorithmus keinen perfekten Spieler und ist an sich uneffizient. Eine sinnvolle Alternative stellt es nicht dar, und ist nach meiner Meinung nicht weiter zu verbreiten. Ein weiterer Ausbau ist nicht möglich und somit, auch nicht verbesserbar.
Trotzdem machte es Spaß sich so einen Spielpartner selbst zu kreieren und die Herausforderung der Programmierung zu bewältigen.

5.Download-Optionen, Kleinigkeiten zum Autor, Quellenverweise

Meine Name ist Lucian Krille. Eigentlich ist nicht viel zu mir zu sagen; wer spricht schon gern über sich selbst? Jedenfalls habe ich eine sehr alte Homepage und einen E-Mail-Anschluß, falls es von Interesse ist.

Mein Programm den Quelltext und die Datenbank gibts hier zum Runterladen. Eine kleine Überraschung ist ebenfalls beigelegt. (kein Virus !!)

zur Gliederung:

:zur Projektseite

2.3        Scrennshots

Mensch gegen PC

Mensch gegen Mensch

Ende, Niederlage Mensch

2.4   Quelltext mit Dokumentation  (aus Platzgründen nur auszugsweise)

Procedure recherche;
Var n,m:Byte;
r:set of byte;
Begin
keine_taktik:=True;
grund_muster(n,m);                (sucht nach Grundtaktiken und setzt sie gegebenenfalls ein)
If Keine_taktik Then Begin
  If vergleich1 Then Begin        (vergleich1 schaut nach, ob es diesen Aufbau schonmal gab)
  n:=3;m:=6;
  Repeat
    Repeat
      Repeat
       dec(m);
       If m=0 Then Begin dec(n); m:=5; End;
       endtest(n,m);                         (Ermöglicht es eine Gegegentaktik? Schreiben in Variable nicht_schlecht)
      Until (ok(n,m)) or (n>3);           (ist der Zug regelkonform )
    Until (nicht_schlecht) or (n>3);
  Until (gibts_nicht(n,m)) or (n>3);    (dieser Zug ist noch nie ausgeführt worden) 
  If n>3 Then Begin n:=0; m:=0; Spielende:=True; Nicht_speichern:=True; End;
End  Else Begin
  r:=[]; 
  For n:=1 To 3 Do If linie[n] > 0 Then r:=r+[n];
    Repeat
      Repeat n:=random(3)+1; Until n in r;
      Repeat m:=random(5)+1; Until linie[n] >= m;
    Until ok(n,m);
  End;
  End;
zug[1]:=n; zug[2]:=m;
End;