(D)
mit a, ai und bi Î N0,
Die folgende Sequenz über Quadratzahlsummen ist als Einstieg in ein Gebiet der Mathematik gedacht, das mit "Zahlentheorie" bezeichnet wird. Diese beschäftigt sich mit den ganzen Zahlen Z={0,± 1,± 2,± 3,..,}. Auf den ersten Blick sieht das ganz einfach aus (keine Brüche, keine Wurzeln,...), doch wird sich schnell herausstellen, dass man in diesem Gebiet einige ganz raffinierte Methoden und einen guten Blick für Problemlösungen benötigt.
Wie man leicht nachprüft, gilt 5=12+22 oder 65=42+72=12+82. Da die Folge der Quadratzahlen immer "löcheriger" wird, stellt sich die Frage, ob man erstens jede natürliche Zahl als Summe zweier Quadrate (wobei wir auch 02 zulassen wollen, um auch die Quadratzahlen zu erfassen) schreiben kann, und zweitens, wie viele solcher Darstellungen es zu jeder Zahl gibt und wie man diese findet
.AUFGABE 1
Stelle die Zahlen von 1 bis 10 als Summe von Quadraten dar.
Schon nach Bearbeitung von nur wenigen Zahlen stellt man fest, dass zwei Quadrate nicht immer reichen. Man braucht aber auch nicht immer mehr Quadrate. Tatsächlich kann man beweisen, dass vier Quadrate für jede Zahl ausreichend sind.
AUFGABE 2
Erweitere die Liste der Quadratsummen bis 61. Versuche auch verschiedene
Darstellungen zu finden.
Die folgenden Sätze der elementaren Zahlentheorie können wir in der Schule nicht beweisen; sie bieten jedoch eine relativ einfache Möglichkeit zu entscheiden, wie viele Quadrate man für die Summendarstellung einer gegebenen Zahl z braucht.
Bevor wir die Sätze angeben, müssen wir eine Klassifikation der Primzahlen angeben, die wir im folgenden benötigen. Alle Primzahlen außer dem "Sonderling" 2 sind ja ungerade. Nun liegen zwischen je zwei Vielfachen von 4 immer zwei ungerade Zahlen; eine direkt nach einem solchen Vielfachen und eine direkt vor einem solchen. Oder anders ausgedrückt: Eine Sorte von ungeraden Zahlen besteht aus den Vielfachen von 4 plus 1 und die andere Sorte aus den Vielfachen von 4 plus 3. Dies gilt nun auch für die Primzahlen:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17..
..Die rot gedruckten Primzahlen sind von der Form p=4k+3, die unterstrichenen von der Form q=4k+1 (Hat man mehrere solcher Zahlen, so bezeichnet man sie mit p1, p2,...bzw. q1, q2,....Man liest p1 als "pee-1". 1 nennt man den "Index" von p.). Diese Bezeichnungsweise wollen wir in diesem Kapitel beibehalten, d.h. eine Primzahl mit dem Namen pi gehört zu denen der Form 4k+3, eine mit dem Namen qi zu denen der Form 4k+1.
AUFGABE 3
Ermittele alle pi und qi bis 100 und stelle sie
als Summe von möglichst wenigen Quadraten dar.
AUFGABE 4
Eine bemerkenswerte Eigenschaft der qi ist die, dass sie
sich alle eindeutig als Summe von zwei Quadraten darstellen lassen - im
Gegensatz zu den pi.
( zuerst von Pierre de Fermat 1640 bewiesen)
Stelle alle qi <200 als Summe von zwei Quadraten dar.
Mit Hilfe der obigen Klasseneinteilung der Primzahlen geben wir nun einen Satz an, der es uns gestattet, direkt zu entscheiden, ob man eine bestimmte Zahl als Summe von nur zwei Quadratzahlen aufschreiben kann oder ob man drei oder gar vier solcher Summanden braucht.
QS 1
Hat eine Zahl zÎ N die Form z=4k(8m+7)
mit k,mÎ N0, so benötigt
man vier Quadratsummanden, um z darzustellen, sonst kommt man mit drei
Summanden aus.
QS 2
Zerlegt man eine Zahl z=a2×r
so, dass r quadratfrei ist, so läßt sich z als Summe von genau
zwei Quadraten genau dann darstellen, wenn r keinen Primfaktor der Form
pi=4k+3 besitzt.
z besitzt dann also die Darstellung
(D) ![]()
mit a, ai und bi Î
N0,
Im Folgenden nennen wir eine Zahl z, die sich nach QS II als Summe von nur zwei Quadratzahlen darstellen läßt ZQZ (Zwei-Quadrate-Zahl). Entsprechend bezeichnen wir Zahlen, die sich nur als Summe von drei Quadraten darstellen lassen, als DQZ und diejenigen, die Summe von vier Quadraten sind, als VQZ. Man beachte, daß bei einer ZQZ alle Exponenten der Primfaktoren p gerade (einschließlich Null) sind.
Beispiele:
34=21·171; 34
ist ZQZ, denn 17 ist von der Form 4k+1 und damit q1 =17 und
b1 =1; tatsächlich gilt: 34=52+32
56=23·7; 56 ist DQZ, denn 7 ist von der Form 4k+3 und damit p1=7 ohne geraden Exponenten, 56=62+42+22
60=4·15=4(8·1+7) ist nach QS I VQZ, 60=72+32+12+12
42=21·31·71
ist DQZ, denn der Exponent von p1=3 ist 1 und damit ungerade;
tatsächlich gilt 42=52+42+12
45=32·5, erfüllt (D), es gilt: 45=62+32
36=22·32 erfüllt (D), 36=62+02
Besondere Probleme bereiten oft die VQZ, daher hier noch einige Beispiele. Besondere Aufmerksamkeit ist immer dann angesagt, wenn in der Primfaktorzerlegung von z der Primfaktor 2 mit geraden Exponenten auftaucht, denn dass ergibt wegen 22k=4k immer eine Viererpotenz.
1776=24·3·37=42·111=
42(13·8+7) ist VQZ
40896=26·32·71=43·639=43
·(79·8+7) ist VQZ
AUFGABE 5
Untersuche alle Zahlen von 70 bis 80 (einschließlich) auf ihre
Darstellung als Quadratzahlsumme mit Hilfe der Kriterien QS I und II.
AUFGABE 6
Ebenso für die Zahlen von 450 bis 455.
AUFGABE 7
Untersuche ebenso die Zahlen von 1985 bis 1995.
Aus der Darstellung (D) kann man auch leicht die Anzahl a(z) der verschiedenen
Darstellungen einer ZQZ ablesen. Es gilt nämlich:
(1) a(z)=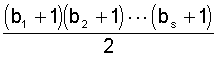 ,
wenn der Zähler gerade ist, und
,
wenn der Zähler gerade ist, und
(2) a(z)=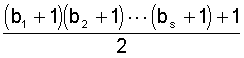 ,
wenn der Zähler in (1) ungerade ist.
,
wenn der Zähler in (1) ungerade ist.
Beispiele:
34=2·17, also b1=1, also a(34)=
![]() =1; 34=52+32
=1; 34=52+32
1985=5·397, b1=b2=1,
also a(1985)=
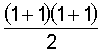 =2 und tatsächlich gilt: 1985=442+72=322+312
=2 und tatsächlich gilt: 1985=442+72=322+312
Bei der Berechnung der verschiedenen Darstellungen einer ZQZ helfen die folgenden Formeln:
(F1) (a2+b2)(c2+d2)=(ac+bd)2+(ad-bc)2
(F2) (a2+b2)(c2+d2)=(ac-bd)2+(ad+bc)2
(F3) (a2+b2)2=(a2-b2)2+(2ab)2
(F4) 2(a2+b2)=(a+b)2+(a-b)2
Die Formeln F1 und F2 lassen sich folgendermaßen deuten: Das Produkt zweier Zahlen, die als Summe von zwei Quadraten darstellbar sind, ist sogar auf zwei Arten als Summe zweier Quadrate darstellbar. F3 und F4 zeigen, wie man das Quadrat bzw. das Doppelte einer Zweiquadratzahl wieder als solche darstellen kann.
Dazu wieder einige Beispiele. Man beachte, dass alle Primzahlen der Form 4k+1 nach (D) ZQZ sind. Man startet deshalb immer mit diesen und gewinnt mit Hilfe der Formeln F1 und F2 daraus immer mehrere Kombinationen. Den Primfaktor 2 packt man bei geradem Exponenten mit zu den (sicher!) quadratischen pi, die wiederum ganz am Ende mit dem Distributivgesetz in die schon gewonnenen Lösungen integriert werden. Hat 2 einen ungeraden Exponenten, so spaltet man einmal 2 ab und benutzt F4.
Beispiel 1:
z=1170=2·32·5·13;
5 und 13 sind von der Form 4k+1, also a(z)=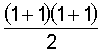 =2;
es gilt 5=22+12 und 13=32+22
=2;
es gilt 5=22+12 und 13=32+22
Dann gilt mit (F1) und (F2):
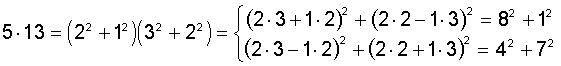
Mit (F4) folgt weiter: 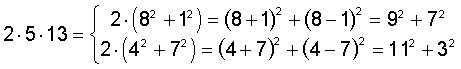
Nun geht´s ganz simpel mit dem Distributivgesetz und der Regel
a2·b2=(a·b)2 weiter:
z=32·(2·5·13)=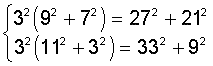
Beispiel 2:
z=750.533=72·172·53,
also a(z)=3; mit (F3) schließen wir
17=42+12 Þ 172=
![]()
172·53=(152+82)(72+42)=
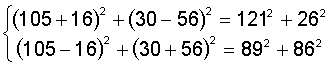
Þ 72·172·53=
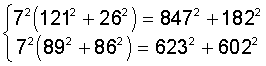
Die dritte Möglichkeit ergibt sich einfach aus:
z=72·172·53=(7·17)2 ·(72+22)=1192·(72+22)=8332+2382
| AUFGABE 8
Untersuche die folgenden Zahlen darauf, wie viele Quadrate für ihre Darstellung nötig sind. Bestimme bei ZQZ auch a(z) und alle möglichen Summendarstellungen: |
|||
| a) 1989 | b) 845 | c) 2.944.414 | d) 6500 |
| e) 414.050 | f) 45.848.349 | g) 5.902.138 | h) 256.360 |
| i) 213.282 | k) 3008 | l) 2.015472 | m) 71.094 |
| n) 53.300 | o) 6.434.296 | p) 28.406.972 | |
|
Und hier noch ein paar schwierige Zerlegungsaufgaben (für den
Computer?):
w) 11.740.625 x) 5.784.025 y) 3.571.838.660 z) 2.372.024.144 |
|||
AUFGABE 9
Bestimme alle Zahlen zwischen 1000 und 1100, die vier Quadrate zu ihrer
Quadratsummendarstellung benötigen.
AUFGABE 10
Als Ergänzung zu den Formeln F1 - F4 sei die folgende, von L.
Euler angegebene Formel genannt:
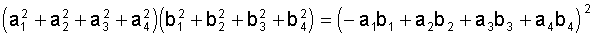 +(a1b2+a2b1+a3b4-a4b3)2+(a1b3-a2b4+a3b1+a4b2)2+
(a1b4+a2b3-a3b2+a4b1)2
+(a1b2+a2b1+a3b4-a4b3)2+(a1b3-a2b4+a3b1+a4b2)2+
(a1b4+a2b3-a3b2+a4b1)2
Diese Formel zeigt uns, dass das Produkt von zwei VQZ wieder als Summe
von vier Quadraten dargestellt werden kann.
Beweise, Beweise, Beweise.....
1) Jede Primzahl p>2 läßt sich eindeutig als Differenz zweier
Quadratzahlen darstellen.
Beweis: Wir versuchen´s einfach mal: p=x2-y2=(x-y)(x+y).
Da p prim ist, muss einer der beiden Faktoren Eins sein (also x-y=1), während
der andere p ist (also x+y=p). Das liefert ein LGS mit 2 Variablen:
(1) x+y=p
(2) x-y=1
Þ 2x=p+1 Ù
2y=p-1 Þ x=
![]() Ù
y=
Ù
y=![]() . Wir haben
damit die beiden gesuchten Quadratzahlen gefunden: p=
. Wir haben
damit die beiden gesuchten Quadratzahlen gefunden: p=
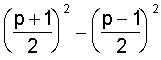
Diese Darstellung gilt übrigens für alle ungeraden Zahlen
p, wie man leicht nachrechnet.
2) Die Summe der Quadrate zweier ungerader Zahlen ist nie ein Quadrat.
Beweis: Es seien a und b zwei ungerade Zahlen, also a=2k+1 und b=2l+1.
Angenommen a2+b2=c2. Dann ist c2
wegen a2+b2=(4k2+4k+1)+(4l2+4l+1)=2(2k2+2k+2l2+2l+1)
sicher gerade und damit auch c gerade. Wir setzen c=2m und erhalten weiter:
a2+b2=(2m)2
2(2k2+2k+2l2+2l+1)=4m2 ï
:2
2k2+2k+2l2+2l+1=2m2
Nun steht auf der linken Seite eine ungerade Zahl, während rechts
eine gerade Zahl steht. Diese Zahlen können daher nicht gleich sein.
Also ist unsere Annahme falsch; es gibt kein c mit c2=a2+b2,
wenn a und b ungerade sind.
Hier haben wir ein schönes Beispiel einer sehr oft verwendeten
Beweistechnik - Beweis durch Widerspruch: Wir nehmen an, dass die Behauptung
zutreffend ist und leiten dann daraus einen Widerspruch zu den Voraussetzungen
ab.
3) z=a2+b2 Ú
z=a2+b2+c2 Þ
z¹ 8d+7 (a,b,c,dÎN)
(in Worten: Wenn zº 7 mod 8, so ist
z nicht Summe von zwei oder drei Quadraten; dies ist ein kleiner Teilbeweis
zu der Behauptung QS I)
Beweis: Auch hier lernen wir ein typisches Beweisprinzip kennen: Wir
teilen die natürlichen Zahlen nach den Resten bei Division durch eine
spezielle Zahl (hier wählen wir dafür 8) ein. Jede natürliche
Zahl läßt bei Division durch 8 entweder den Rest 0, 1, 2, 3,
4, 5, 6 oder 7. Dann lassen die Quadrate dieser Zahlen bei Division durch
8 der Reihe nach die Reste 0, 1, 4, 1, 0, 1, 4, oder 1 (es treten also
nur noch die drei verschiedenen Reste 0, 1 und 4 auf).
Nun schauen wir uns an, welche Reste die Summe von zwei bzw. drei solcher
Quadratzahlen bei Division durch 8 läßt. Fangen wir mit zwei
Summanden an: 0+0=0; 0+1=1; 0+4=4; 1+1=2; 1+4=5; 4+4=8 (was wieder dem
Rest 0 entspricht). Es bleibt nie der Rest 7, und das ist ja die Behauptung.
Um nicht so viele verschiedene Fälle bei drei Summanden betrachten
zu müssen, machen wir uns zunächst klar, dass wir die Summe von
drei geraden Resten oder zwei ungeraden Resten mit einem geraden Rest außer
Acht lassen können, denn diese Summen sind sicher gerade und damit
nicht 7. Wir haben damit nur noch vier Fälle zu betrachten: 0+0+1=1;
0+1+4=5; 1+1+1=3; 1+4+4=9 (was dem Rest 1 entspricht). Also ergibt sich
auch bei drei Summanden nie der Rest 7.
4) z=a2+b2 Þ
z¹ 4n+3
Beweis: Angenommen, es gebe doch eine Zahl z=4n+3, die als Summe von
a2 und b2 darstellbar ist. Dann muss eine der beiden
Zahlen a oder b gerade und die andere ungerade sein, da anderenfalls ihre
Summe gerade wäre. Es sei also a=2k und b=2l+1. Dann folgt aus a2+b2=4n+3
:
(2k)2+(2l+1)2=4n+3
4k2+4l2+4l+1=4n+3
4(k2+l2+l)=4n+2
2(k2+l2+l)=2n+1 #
Nun steht links eine gerade Zahl und rechts eine ungerade Zahl. Das
ist nicht möglich - die Annahme ist also falsch.
AUFGABE 11
Setze die Reihe der Gleichungen fort. Formuliere danach eine Vermutung
und beweise diese.
22+32+62 =72
32+42+122=132
42+52+202=212
AUFGABE 12
Setze die Reihe der Gleichungen fort. Formuliere danach eine Vermutung
und beweise diese.
23=32-12
33=62-32
43=102-62
53=152-102
AUFGABE 13
Für Spezialisten:
6(a2+b2+c2+d2)2=
(a+b)4+(a+c)4+(a+d)4+(b+c)4+(b+d)4+(c+d)4
+(a- b)4+(a-
c)4+(a- d)4+(b-
c)4+(b- d)4+(c-
d)4
(Die Sache ist nur halb so schwierig, wenn man zunächst mal
(x+y)4+(x-y)4 vereinfacht.)
Ein Ausflug in die Mathematikgeschichte:
Im Jahre 1778 erwähnte L.Euler (1707 - 1783; Schweizer Mathematiker)
in einem Brief die Vermutung, dass man die n-te Potenz einer Zahl nicht
als Summe von weniger als n n-ten Potenzen erhalten könne. So ist
z.B. 93=13+63+83 oder 63=33+43+53.
Diese Vermutung wurde gemeinhin als richtig angesehen, bis Landau und
Parker 1966 mit dem Beispiel 275+845+1105+1335=1445
Euler
widerlegten.
Der französische Mathematiker Liouville bewies im 19.Jahrhundert (übrigens unter Zuhilfenahme der Formel aus Aufgabe 14), dass sich jede Zahl als Summe von höchstens 53 Biquadraten (vierten Potenzen ) darstellen läßt.
 Download Kap 0(19 KB)
Download Kap 0(19 KB)

Copyright © Michael Dorner, Sept. 2000.