15-Puzzle

Das 15-Puzzle wurde gegen Ende des 19. Jahrhunderts von dem US-amerikanischen Postangestellten Noyes Palmer Chapman erfunden. Auf einem 4×4-Spielfeld lassen sich 15 Kacheln mit den Nummern 1 bis 15 verschieben. Das Ziel des Spiels besteht darin, aus einer vorgegebenen (ungeordneten) Stellung die geordnete Ausgangsstellung wiederherzustellen.

Nach der Formel für Permutationen gibt es 16!   =   1 · 2 · 3 · ... · 14 · 15 · 16   =   20.922.789.888.000 Möglichkeiten, die 15 Kacheln und das leere Feld auf dem Spielfeld zu platzieren. Allerdings ist die gestellte Aufgabe in der Hälfte dieser Fälle unlösbar. Daher ist die Zahl der möglichen Stellungen 10.461.394.944.000.

Um herauszufinden, ob für eine gegebene Stellung die Lösung möglich ist, verwendet man den sogenannten Umordungsparameter N₁ und den Reihenparameter N₂.

• Beim Umordnungsparameter betrachtet man alle Zahlenpaare (m,n) mit m < n, also die Paare (1,2), (1,3), ..., (1,15), (2,3), (2,4), ..., (2,15), (3,4), ..., (14,15). Die angestrebte Ordnung sei durch Pfeile veranschaulicht. Zählt man nun diejenigen Zahlenpaare, bei denen die zweite Zahl in Richtung der Pfeile zuerst kommt, so erhält man den Umordnungsparameter N₁.
• Der Reihenparameter N₂ ist die Nummer der waagrechten Reihe, in der sich das leere Feld befindet.

Das Problem ist für eine bestimmte Anfangsstellung genau dann lösbar, wenn die Summe N₁ + N₂ eine gerade Zahl ist.

Beispiel:

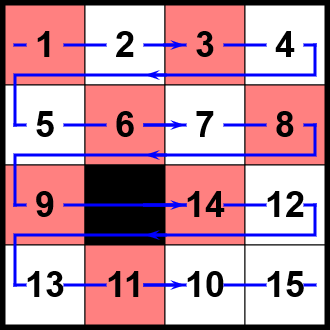
In der abgebildeten Stellung haben die folgenden 9 Zahlenpaare eine "falsche" Reihenfolge: (10,11), (10,12), (10,13), (10,14), (11,12), (11,13), (11,14), (12,14), (13,14). Der Umordnungsparameter N₁ hat demnach den Wert 9. Das leere Feld befindet sich in der 3. Reihe, es gilt also N₂ = 3. Weil N₁ + N₂ = 9 + 3 = 12 eine gerade Zahl ist, ist die Aufgabe für diese Anfangsstellung lösbar.

Quelle: Wikipedia (deutsch), Artikel "15-Puzzle"