Mustererkennung

Im Jahre 2007 wurde im Mainzer Hauptbahnhof ein aufwändiges Experiment durchgeführt: Alle Personen, welche das Gebäude verließen, wurden von Kameras erfasst; automatisiert wurde die jeweilige Physiognomie mit den Daten von 50 Testpersonen verglichen. Der Versuch war nicht erfolgreich, da man  eine höhere Erkennungsrate erwartet hatte; die verwendeten Suchalgorithmen waren allerdings nicht das Problem, sondern schlicht und ergreifend die Tatsache, dass die Lichtverhältnisse im Bahnhof abends nicht ausreichend sind: Menschen, nach denen gefahndet wird, lassen sich nun mal nicht vorschreiben, am Tage zu reisen (vgl. auch den Abschlussbericht des BKA   ).

                                                                                                                                                                                                                                                                                                                                           Foto: dpa

Die Mustererkennung ist nicht nur ein Teilgebiet der Informatik, sondern sie hat schon sehr früh  die Technik und unseren Alltag bestimmt:                                                                                                                                                                                                                              

• Schon als studentischer Briefträger in den siebziger Jahren stellte ich Briefe zu, auf denen Codes zur automatischen Vorsortierung aufgedruckt waren.

• Unsere Schulsekretärinnen verwenden schon seit 1995 Spracherkennung zur Eingabe ihrer Texte.

• Als wir 1989 für viel Geld einen Schwarz-Weiß-Scanner bekamen, kostete die Software zur Text- (Buchstaben-)erkennung (Recognita) noch mal soviel und war durch Dongle geschützt.

• Zur Aufklärung von Gewalttaten werden am Tatort gefundene DNA-Spuren mit den DNA-Codes Verdächtiger abgeglichen.

Die Liste mit Beispielen zum "Pattern Matching" (Musterabgleich) ließe sich noch beliebig ergänzen, wenn wir z.B. an das Scannen unserer Autonummern auf der Autobahn (offiziell nur, um säumige LKW-Fahrer zu entdecken), an Viren-Scanner (die ja auch die Codes von Schadprogrammen entdecken sollen) oder an das Suchen im Text oder im Internet via Suchmaschine denken. Auch beim Decodieren von Text arbeitet man in der Kryptologie gelegentlich mit Pattern Matching.

Die Aufgabenstellung
Für die Praxis lässt sich die Mustererkennung auf der Ebene des digitalen Suchens beschreiben: 
                               Eine Bitstruktur gegebener Länge  soll in einer längeren Dualzahl gefunden werden.

Bereitstellung von Feldern als wesentliches Werkzeug zur Mustererkennung
Wir benötigen geeignete "Container", in die wir das Bit-Muster und den Suchbereich eingeben können. Diese flexibel adressierbaren Container müssen unter einem Namen für jedes Bit einen Integer-Speicherplatz vorsehen und den direkten Zugriff auf das einzelne Bit ermöglichen. 
Ein solcher strukturierter Datentyp heißt Feld oder ARRAY.
Wir betrachten ein Integer-Feld der Länge 3:

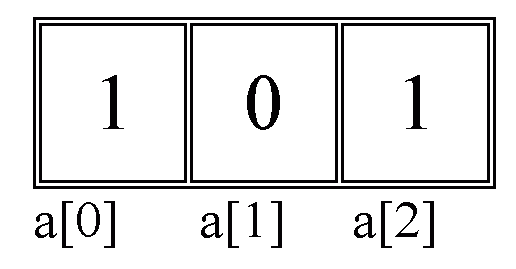
Gewöhnungsbedürftig ist, dass der erste Feldplatz mit dem Index 0 angesprochen wird und der dritte entsprechend mit dem Index 2.

Der Benutzer liest ein Feld mit beliebigen Integerzahlen ein

import java.util.Scanner;
class Feld  {
  public static void main(String[] args)  {
    Scanner s = new Scanner (System.in);
    int n;
    // Eingabeschleife für Feldlänge; läuft bis Eingabewert im gültigen Bereich
    do {
      System.out.println("Wie viel Feldelemente sollen eingelesen werden? (hoechstens 10)");
      n = s.nextInt();
    }
    while ((n < 1) || (n > 10));

    int[] a = new int[n];
    // Eingabe
    for (int i = 1; i <= n; i++) {
      System.out.printf("%n%d.tes Feldelement als ganze Zahl   ",i);
      a[i - 1] = s.nextInt();
    } 
    // Ausgabe 
    for (int i = 1; i <= a.length; i++) 
      System.out.printf("%nDas %d.te Feldelement ist %d  ",i, a[i - 1]);
  }
}

Bemerkungen:

• Der Benutzer legt erst zur Laufzeit auch die Dimensionierung des Feldes fest
• Eine Eingabeabsicherung immerhin für den Größenbereich wurde realisiert
• Die Feldgröße ist über a.length abrufbar.

Im Hinblick auf das Ziel dieses Kapitels werden wir jetzt größere Felder mit Zufalls(dual-)zahlen füllen.

Per Zufallsgenerator Felder mit Dualzahlen füllen

import java.util.Scanner;
class Feld   {
  public static void main(String[] args)  {
    Scanner s = new Scanner (System.in);
    int n;
    // Eingabeschleife für Feldlänge
    do {
      System.out.println("Wie viel Feldelemente sollen eingelesen werden? (hoechstens 10)");
      n = s.nextInt();
    } 
    while ((n < 1) || (n > 10));
    int[] a = new int[n];
    // Eingabe
    for (int i = 1; i <= a.length; i++) 
      a[i - 1] = (int) Math.floor(Math.random() * 2);

    // Ausgabe 
    for (int i = 1; i <= a.length; i++) 
      System.out.printf("%nDas %2d.te Feldelement ist %d  ",i, a[i - 1]);
  }
}
    

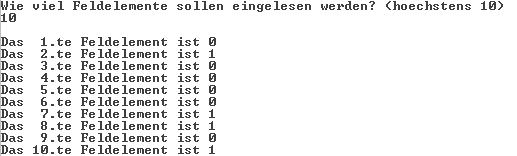
Den Zufallsgenerator haben wir schon in letzten Kapitel  benutzt. Wenn man Math.random()verdoppelt und mit Math.floor
die Nachkommastellen abschneidet, erhält man 0 und 1 als Zufallszahlen. (Der Typ int wird erzwungen, da es sonst Typ-Konflikte mit dem Typ long gäbe).

Suchbereich und Suchmuster realisieren

import java.util.Scanner;
class Feld  {
  public static void main (String[] args)   {
    Scanner s = new Scanner (System.in);
    int n,m;
    do {
       System.out.println("Wie viel Feldelemente soll der Suchbereich enthalten (hoechstens 20)");
      n = s.nextInt();
      System.out.println("Wie viel Feldelemente soll das Suchmuster enthalten (hoechstens 5)");
      m = s.nextInt();
    }
    while ((n < 1) || (n > 20) || (m < 1) || (m > 5));
    System.out.printf("Grosses Feld der Laenge %d, kleines Feld der Laenge %d%n",n,m);
    int[] a,b;

    a = new int[n];
    b = new int[m];

    //Felder füllen
    for (int i = 0; i < n; i++)
      a[i] = (int) Math.floor(Math.random()*(2));
    for (int i = 0; i < m; i++)
      b[i] = (int) Math.floor(Math.random()*(2));  

    // Ausgabe; 
    for (int i = 0; i < n; i++)
      System.out.printf("%3d",a[i]);
    System.out.printf("%n%n"); 
 
    for (int i = 0;i < m; i++)
      System.out.printf("%3d",b[i]);
    System.out.println();    
  }
}

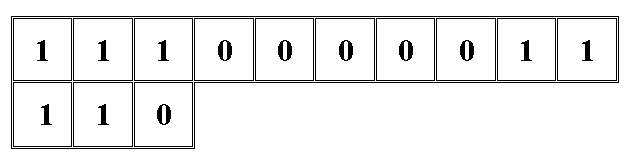
Wenn wir paarweise die jeweils ersten 3 Feldelemente vergleichen, haben wir beim ersten Durchgang keinen Erfolg. Also werden wir das Suchmuster eine Stelle nach rechts schieben.

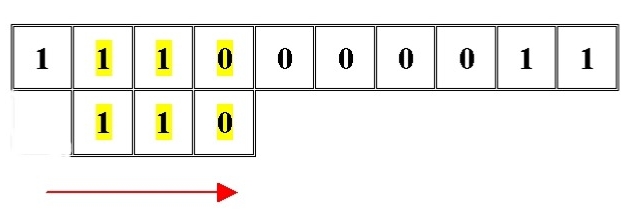
In diesem Fall müssen wir ausgeben, dass wir das Suchmuster ab dem Index 1 im Suchfeld 

gefunden haben. Entsprechend sind 6 weitere Durchgänge möglich, aber das Suchmuster wird in diesem Fall nicht mehr gefunden

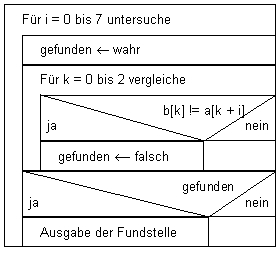
Das Struktogramm nutzt Wahrheitswerte; diese stehen über dem Datentyp boolean zur Verfügung; 
für eine Variable dieses Typs gibt es nur die Werte true oder false.

// Anfang wie oben; (klein gedruckt)

import java.util.Scanner;
class Feld {
public static void main (String[] args)   {
Scanner s = new Scanner (System.in);
int n,m;
do {
  System.out.println("Wie viel Feldelemente soll der Suchbereich enthalten (hoechstens 20)");
    n = s.nextInt();
    System.out.println("Wie viel Feldelemente soll das Suchmuster enthalten (hoechstens 5)");
    m = s.nextInt();
 }
 while ((n < 1) || (n > 20) || (m < 1) || (m > 5));
System.out.printf("Grosses Feld der Laenge %d, kleines Feld der Laenge %d%n",n,m);
int[] a,b;
a = new int[n];
b = new int[m];
//Felder füllen
for (int i = 0; i < n; i++)
  a[i] = (int) Math.floor(Math.random()*(2));
for (int i = 0; i < m; i++)
  b[i] = (int) Math.floor(Math.random()*(2));  
// Ausgabe; 
for (int i = 0; i < n; i++)
  System.out.printf("%3d",a[i]);
System.out.printf("%n%n"); 
for (int i = 0;i < m; i++) 
  System.out.printf("%3d",b[i]);
System.out.println(); 

// Suchbereich durchmustern 
for (int i = 0; i <= n - m; i++) {
  // Zunächst gehen wir davon aus, dass das Suchmuster gefunden wird
  boolean gefunden = true;
  for (int k = 0; k < m; k++)
     if (b[k] != a[i+k])
        gefunden = false;
  if (gefunden) 
     System.out.printf("Das Suchmuster wurde ab dem Index %d im Suchbereich gefunden%n",i);          
  }  
 }
}

Zeichenketten kann man über + verknüpfen; diese Konkatenation ist polymorph, d.h. Zahlen werden ohne  Transformation in den String eingebaut;
also ist möglich:
                                   text = text + 1; 

Wir nutzen dies, um unser Zahlenmuster in eine Stringvariable zu packen, welche wir bei der Meldung einsetzen können.

Außerdem kann man das Ergebnis einer relationalen Operation direkt (ohne if-Abfrage) einer booleschen Variable zuweisen.
Schließlich kann man mit einer zweiten booleschen Variable überwachen, ob das Suchmuster ggf. bei keinem Suchlauf gefunden wurde.

// Anfang wie oben; (klein gedruckt)

import java.util.Scanner;
class Feld_5 {
public static void main (String[] args)   {
Scanner s = new Scanner (System.in);
int n,m;
do {
  System.out.println("Wie viel Feldelemente soll der Suchbereich enthalten (hoechstens 20)");
    n = s.nextInt();
    System.out.println("Wie viel Feldelemente soll das Suchmuster enthalten (hoechstens 5)");
    m = s.nextInt();
    }
 while ((n < 1) || (n > 20) || (m < 1) || (m > 5));
System.out.printf("Grosses Feld der Laenge %d, kleines Feld der Laenge %d%n",n,m);
int[] a,b;
a = new int[n];
b = new int[m];
//Felder füllen
for (int i = 0; i < n; i++)
  a[i] = (int) Math.floor(Math.random()*(2));
for (int i = 0; i < m; i++)
  b[i] = (int) Math.floor(Math.random()*(2));  
// Ausgabe; 
for (int i = 0; i < n; i++)
  System.out.printf("%3d",a[i]);
System.out.printf("%n%n");  
String suchmuster = "";
for (int i = 0;i < m; i++) {
  System.out.printf("%3d",b[i]);
  suchmuster = suchmuster + b[i];
}
System.out.println(); 
// Suchbereich durchmustern
// zunächst noch nichts gefunden
boolean nix_drin = true;
for (int i = 0; i <= n - m; i++) {
  // Zunächst gehen wir davon aus, dass das Suchmuster in diesem Durchgang gefunden wird
  boolean gefunden = true;
  for (int j = 0; j < m; j++)
     gefunden = ((b[j] == a[i+j]) && (gefunden));
  if (gefunden) {
     System.out.printf("Das Suchmuster "+suchmuster+" wurde ab dem Index %d im Suchbereich gefunden%n",i); 
     nix_drin = false;
     }         
   } 
if (nix_drin)
  System.out.println("Das Suchmuster "+suchmuster+" wurde in keinem Durchgang gefunden"); 
 }
}

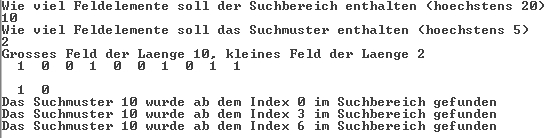
oder:

Effizientes Programmieren

Eigentlich ist das Suchen über die ganze Länge m des Suchmusters nicht effektiv, wenn schon am Anfang eines Suchdurchgangs klar ist, dass es keine Übereinstimmung geben wird (vgl. unser Einstiegsbeispiel beim 4. Durchgang). Wir müssen uns also wieder mal von der Starrheit der Zählschleife lösen. Eine while-Schleife und die geschickte Kombination von logischen Ausdrücken und booleschen Variablen lösen das Problem:

// Anfang wie oben; (klein gedruckt)

import java.util.Scanner;
class Feld_6 {
public static void main (String[] args)   {
Scanner s = new Scanner (System.in);
int n,m;
do {
  System.out.println("Wie viel Feldelemente soll der Suchbereich enthalten (hoechstens 20)");
    n = s.nextInt();
    System.out.println("Wie viel Feldelemente soll das Suchmuster enthalten (hoechstens 5)");
    m = s.nextInt();
      }
 while ((n < 1) || (n > 20) || (m < 1) || (m > 5));
System.out.printf("Grosses Feld der Laenge %d, kleines Feld der Laenge %d%n",n,m);
int[] a,b;
a = new int[n];
b = new int[m];
//Felder füllen
for (int i = 0; i < n; i++)
  a[i] = (int) Math.floor(Math.random()*(2));
for (int i = 0; i < m; i++)
  b[i] = (int) Math.floor(Math.random()*(2));  
// Ausgabe; 
for (int i = 0; i < n; i++)
  System.out.printf("%3d",a[i]);
System.out.printf("%n%n");  
String suchmuster = "";
for (int i = 0;i < m; i++) {
  System.out.printf("%3d",b[i]);
  suchmuster = suchmuster + b[i];
}
System.out.println(); 
// Suchbereich durchmustern
// zunächst noch nichts gefunden

boolean nix_drin = true;
for (int i = 0; i <= n - m; i++) {
  // Zunächst gehen wir davon aus, dass das Suchmuster in diesem Durchgang gefunden wird
  boolean gefunden = true;
  int j = 0;
     //Jetzt wird der Suchvorgang direkt abgebrochen, wenn ein Bit nicht übereinstimmt
  while ((gefunden) && (j < m)) {
     gefunden = ((b[j] == a[i+j]) && (gefunden));
     j++;
  }
  if (gefunden) {
     System.out.printf("Das Suchmuster "+suchmuster+" wurde ab dem Index %d im Suchbereich gefunden%n",i); 
     nix_drin = false;
     }         
   } 
if (nix_drin)
  System.out.println("Das Suchmuster "+suchmuster+" wurde in keinem Durchgang gefunden"); 
 }
}

Quellen

1. Vorlesung "Einführung in die Programmierung" von Prof. Dr. Herbert Göttler im WS 2007 / 2008 an der Universität Mainz.
   
2. Übungsblätter "Einführung in die Programmierung" von Thomas Gottron im WS 2007 / 2008 an der Universität Mainz.
   
3. Reinhard Schiedermeier — Programmieren mit Java  ISBN: 978-3-8273-7116-4
   480 Seiten; Sprache: Deutsch; € 39,95 [D]
   
4. Herrn Mahdi D-Manesh / Universität Mainz / Fachbereich Informatik bin ich für die Durchsicht der Vorlage und die 
   hilfreichen Anregungen sehr dankbar.