Übungen: Zeitgleichung

Die wahre Sonne bewegt sich dagegen auf der Ekliptik, die um ca. 23,5º gegen den Himmelsäquator geneigt ist. Ferner führt sie auf der Ekliptik keine gleichförmige sondern eine ungleichförmige Bewegung, die sich aus der Ellipsenbewegung der Erde um die Sonne ergibt.

Die wahre Sonne kulminiert um 12 h WOZ (wahre Ortszeit). Die Differenz zwischen Zeitpunkt des mittleren Mittags und dem Zeitpunkt des wahren Mittags nennt man Zeitgleichung. Sie nimmt für jeden Tag des Jahres einen anderen Wert an. Es gilt:

Ist Ztgl < 0, so geht die wahre Sonne verspätet durch den Meridian, eine (einfache) Sonnenuhr geht nach, ist Ztgl > 0, so geht die wahre Sonne zu früh durch den Meridian, eine Sonnenuhr geht vor.

Aufgaben:

1. Machen Sie sich an einer Kugel klar, dass bei einer gleichförmigen Bewegung der Sonne auf der Ekliptik die Abschnitte von Stundenkreis zu Stundenkreis ungleichmäßig durchlaufen werden.

Begründen Sie, dass deshalb die Schiefe der Ekliptik allein schon zu einer Asynchronität zwischen mittlerer und wahrer Sonne führt, (die dann noch durch die ungleichförmige Bewegung der Erde auf der Ekliptik überlagert wird.)

2. Die Sonnenauf- bzw. Untergangszeiten sind im Kalender meist für einen "geographischen Mittelwert (10⁰ E; 51⁰ N)" angegeben. Dies entspricht etwa Kassel.

Ermitteln Sie in der beigefügten Tabelle jeweils den Zeitpunkt des wahren Mittags (in MEZ) für Kassel (näherungsweise) als Mittelwert zwischen dem Zeitpunkt von Sonnenauf- und untergang.

3. Zeichnen Sie Auf- und Untergangszeiten und den Zeitpunkt des wahren Mittags in ein geeignetes Koordinatensystem ein. (DIN A4 Querformat)
4. Warum ist der Mittelwert des "wahren Mittags" für 10⁰ E nicht 12.00 Uhr ?
5. Um wie viel Uhr MEZ muss demnach der "mittlere Mittag" für 10⁰ E erfolgen ?
6. Berechnen Sie die Zeitgleichung für die einzelnen Tage in der beigefügten Tabelle aus dem Zeitpunkt der wahren Mittags.
7. Zeichnen Sie ein Schaubild für die Zeitgleichung.
8. Die Zeitgleichung hat zwei Ursachen: Die Schiefe der Ekliptik und die Ellipsenbewegung der Erde auf der Ekliptik.

Zeigen Sie:
1. Der Einfluss der Ellipsenbewegung hat die Periode 1 Jahr.
2. Der Einfluss der Schiefe der Ekliptik hat die Periode 0,5 Jahre.
9. Versuchen Sie eine Näherungsformel für die Zeitgleichung aufzustellen, die die Form

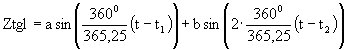
hat. Bestimmen Sie die Parameter so, dass die maximale Abweichung zu den berechneten Werten möglichst gering wird.

Die nachfolgenden Ausgangsdaten als Textfile laden. (Speichern Sie den File unter Zeitglei.txt,  und bearbeiten Sie die Aufgabe mit Hilfe einer Tabellenkalkulation, in die Sie Zeiglei.txt einlesen)

Sonnenauf-/untergangszeiten 1990 für Kassel (10^o E; 51^o N)